２章課題

五角形は、方向を5回変えたときに360度回っていればいいんだから、360÷5を計算して、72度回転すればいいことがわかるね。だからスクリプトはこうなるよ。

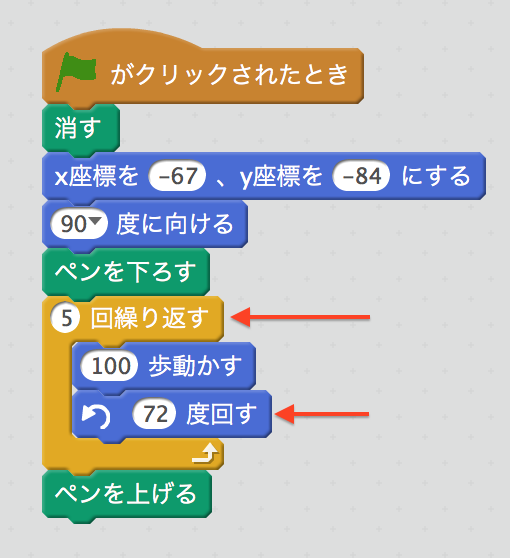
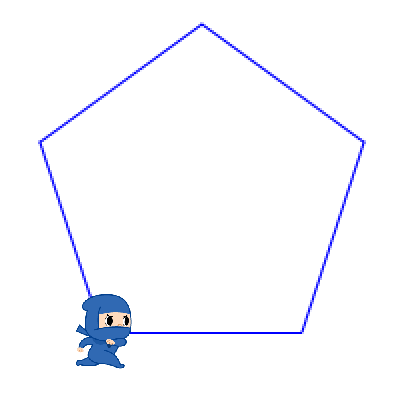
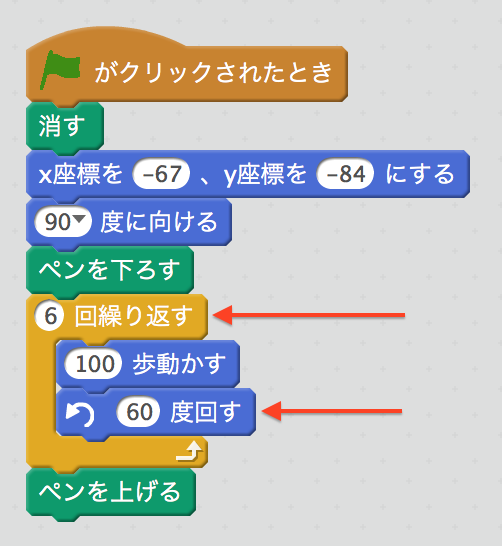
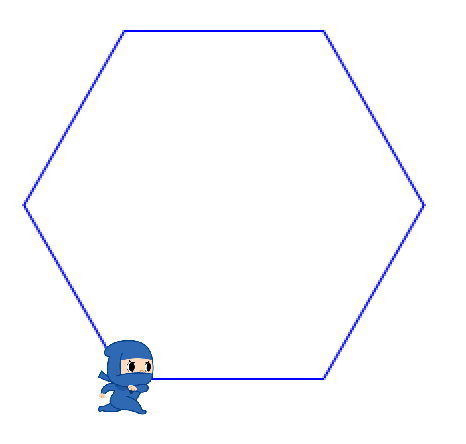
六角形は、実はタカシくんが途中までかいていたね。気がついたかな?　65ページで三角形をかくのに失敗していたのが、ちょうど六角形の半分になっていることを確認してみよう。もう半分をかけばいいのだから、こうなるよ。

第4章を読みおえている人へ

五角形をかいたときに回転した72度は360÷5だったし、六角形をかいたときに回転した60度というのは360÷6だった。どっちもわり算のブロック 「○/○」 でおきかえることができるね。そうしたときのブロックを見てみよう。

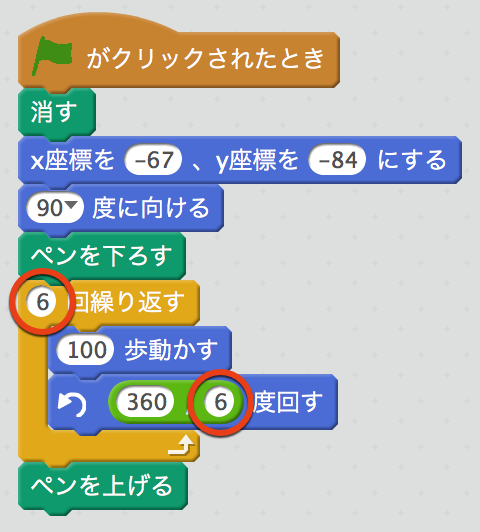
上のような形になるけれども、○で囲った2つにはいつも同じ数字がはいるね。こんなふうに同じ数字をくりかえして使うときも、変数を使うといいんだ。

そうするとこんなふうになる。

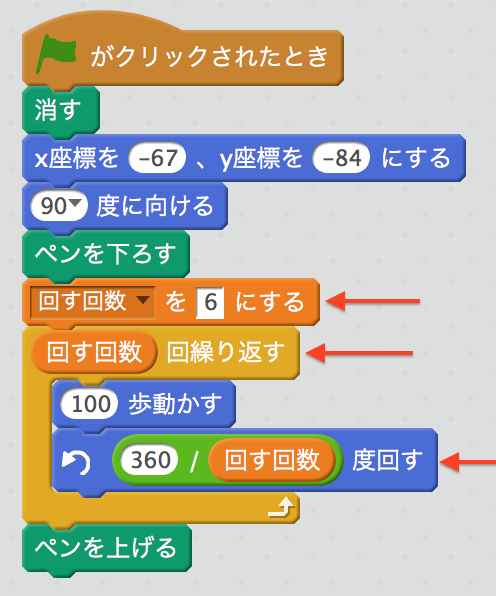
まだ、進む歩数は調整しないといけないけど、これでずいぶん楽になったよね!

課題2：360度にならないように回転するとどうなるだろう？

課題内容（書籍P.78）

回転の合計が360度になるように回転すると正三角形や正方形をかくことができた。

では、350度ぴったりにならないような回転をするとどうなるんだろうか？

たとえば、 「100歩動かす」 や 「100度回す」 をくりかえしたとき、何回くりかえしたら元の場所にもどって来るだろうか？ 元の場所にもどって来たとき、どんな図形がかかれているか、たしかめてみよう！

いつかは成功するかもしれないけれど、何回くりかえせばちょうどいいのかわからない場合、どうすればいいかな？

いくつかやりかたがあるよ。

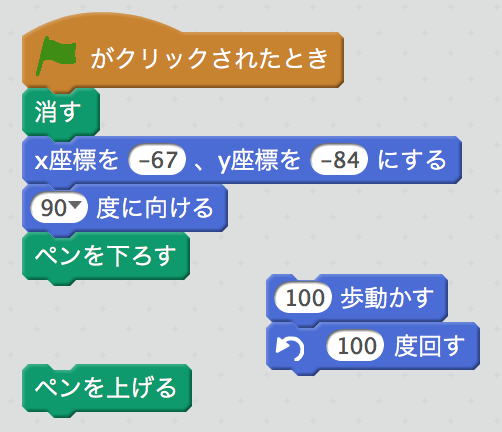
手で数える

こういうスクリプトを配置して、自分で 「100歩動かす」 と 「100度回す」 をクリックしてみてようすをみてみよう。何回くりかえしたらいいかは自分で数えることになるね。

くりかえすをくりかえし試す

本で説明したような、こんなスクリプトを作っておいて、くりかえす回数を少しずつふやしていって試してみることもできるね。

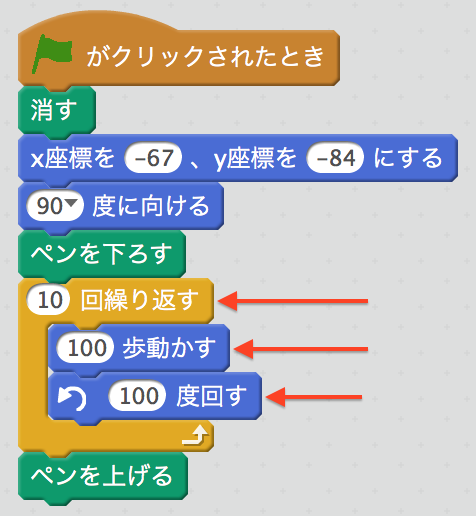
答えは18回だ 。18回くりかえすと、元の場所にもどってくるよ。

こういう図形がかかれたね。

ほかにも、いろんな角度でためしてみて、いろんな図形をかいてみよう。回転する角度は、1の位が5か0になるような数字にするといいよ。

第4章を読みおえている人へ

元の方向（右向き）にもどったかどうかを、 「もし〜なら」 のブロックでチェックすることができるよ。

くりかえしの回数を決めなくても、こういうスクリプトを書くといいんだ。

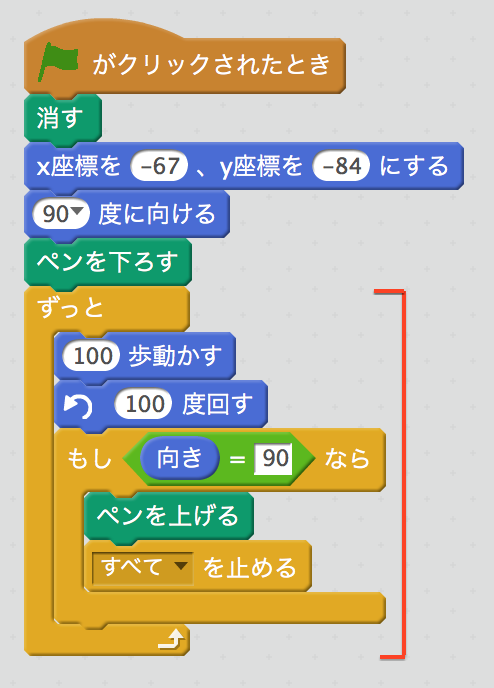
元の方向にもどったときには、いつも元の場所にもどってくるんだろうか？　これもいろんな角度でためしてみてね。